__DS & OOP

OPP 란?

객체 지향 프로그래밍이란(OOP: Object Oriented Programming)?

  • 객체들의 모임이다.

객체 지향 프로그래밍 장점

  • 코드의 재사용성 제공 *객체의 특성이나 속성을 한 번 정의해 놓으면 해당 객체에 소속되어 있는 모든 객체들의 속성으로 사용할 수 있으므로 재사용성이 높아진다.
  • 유지보수의 용이 : 한 번만 정의한 것을 수정하면 모든 객체의 속성을 수정할 수 있다.
  • 신뢰성 증대 : 다양하게 사용된 속성들에 경험이 쌓이면서 신뢰가 축적되기 쉽고 그것을 다시 사용한다면 에러(버그)의 가능성이 줄어든다.

OOP의 기본 구성 요소

  • 클래스(Class)

  • 객체(Object)

  • 메서드(Method)

OPP 기본 컨셉 4 가지 있다.

    1. 캡슐화(Encapsulation)
    1. 상속(Inheritance)
    1. 추상화(Abstraction)
    1. 여러가지 형태 (Polymorphism)

1.캡슐화란?

  • 속성들(properties)들을 object안에 넣어서 활용한다.

  • 예시

employee라는 객체 안에 객체들을 넣어서 사용한다. 이것이 캡슐화이다.


let baseSalary = 3001;
let overTime = 10;
let rate = 20;

function getwage(baseSalary,overTime,rate) {
return baseSalary + (overTime * rate);
}

getwage() // NaN 
getwage(baseSalary,overTime,rate) // 3200
  • 캡슐화 한 코드


let employee = {
	baseSalary : 3000,
	overTime : 10,
	rate: 20,
	getWage: function() {
	return this.baseSalary + (this.overTime * this.rate);
	}
 }
 
 employee.getWage();// 3200

2.상속?

  • 상속은 쉽게 말하면 상위 클래스의 모든 것, 행동을 하위 클래스가 가지고 있으며 그대로 사용할 수도 있고 원하면 Customizing을 할 수 있다는 것이다.
  • 부모 클래스가 가지고 있는 속성(프로퍼티, 메소드) 등을 그대로 자식 클래스가 물려 받아 재사용이 가능하다.

3.추상화란?

  • 속에는 복잡하게 되어있지만 사용자가 쓰기에는 굉장히 간단하다.
  • 인터페이스가 간단해진다.
  • 복잡한걸 알지않아도 사용자 입장에서는 사용 가능

4.여러가지 형태 다양성 ?

  • 다형성은 상속을 받은 기능을 변경하거나 확장하는 것
  • 코드의 재사용성이 높아져 코드의 길이가 감소하고 유지보수가 용이해짐

prototype 무엇이냐?

자바스크립트는 프로토타입 기반 객체지향 프로그래밍 언어이다.

  • ES6 문법이 도입되기 전에는 JavaScript에는 클래스(Class)가 없었음 그래서 객체 생성을 위해서 prototype을 사용했다.

  • 객체를 생성하면, 프로토타입이 결정되고, 우리는 그 프로토타입을 변경할 수 있습니다

첫번째 알아야 할것

  • 함수를 만들어 변수에 담을때 new 라는 것을 같이 담으면 객체가 된다.

function Person() {}

let x = new Person(); //  x 라는 변수는 객체가 된다.

두번째 알아야할 것

  • 객체(object)는 함수(function)로부터 시작된다

function Book() { }                // 함수 <<생성자 함수
var jsBook = new Book();           // 객체 생성
  • 두가지 방식을 객체를 생성할수 있다.
var jsBook = new Book(); // 첫번째 방식 (생성자 함수) // 객체 

var jsBook = {}          // 두번째 방식(생성자 선언 없이 ) // 객체

세번째 알아야 할것

  • 함수 생성시 발생하는 것을 알아야 한다.

    • 1.함수를 정의하면 함수가 생성되며 Prototype object가 같이 생성 됩니다.

생성된 Prototype object는 함수의 prototype 속성을 통해 접근할 수 있습니다. (Prototype object같은 경우 함수 생성시(var jsBook = new Book())에만 됩니다. 일반 객체 생성시에는 생성되지 않습니다.)

  • 2.함수의 생성과 함께 생성된 Prototype object는 constructor와 __proto__를 갖고 있습니다.

constructor는 생성된 함수를 가리키며(여기서는 function Book을 가리킵니다.)

__proto__는 Prototype Link로서 객체가 생성될 때 사용된 생성자(함수)의 Prototype object를 가리킵니다.

네번째 알아야 하는것

  • 객체(object) 생성시 발생하는 일

생성하는 순간 jsBook 이라는 객체는 proto 라는 _proto__라는 프로퍼티를 갖고있습니다.


function Book() { }

Book.prototype.name = "john" 

var jsBook = new Book() // jsBook 은 객체이다.

prototype property(함수 생성시 함께 생성된 Prototype object를 가리킴)는 함수객체만 가지며 __proto__는 객체라면 모두 갖고 있습니다.

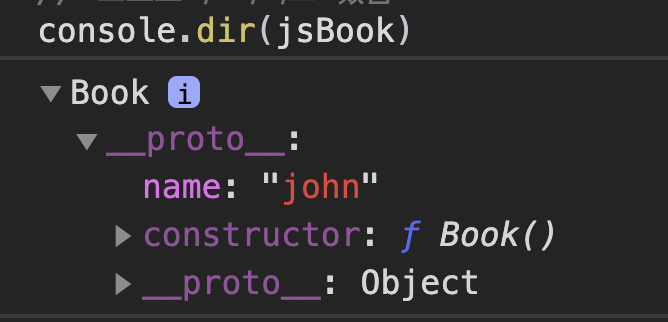
![](/tutorial/2019-11-26-js-post_files/Screen Shot 2019-12-16 at 2.39.56 PM.png)

prototype property(함수 생성시 함께 생성된 Prototype object를 가리킴)는 함수객체만 가지며 __proto__는 객체라면 모두 갖고 있습니다.

예제)

  • 1.일반적인 함수 패턴



function Name(_name){
    var oName = {
        name : _name,
        getName : function(){
            return this.name;
        }
    }

    return oName;
}

Name('john'); // Object{name: 'siwa', getName:function()} 리턴
var x = Name('john');
x.getName(); // 'john' 리턴

  • 1.객체 생성자 함수의 활용 - 모듈화,프로토타입

    • new Key word 를 사용한다.

    • 이는 객체지향적인 언어를 표방하는 기능, 클래스를 만드는 것과 비슷하다.

    • (new라는 키워드는 자바에서 클래스를 호출해서 인스턴스를 만드는 것과 비슷하다)


 function Name(_name){
		console.log('this is',this);
		this.name = _name;
		this. getName = function(){
        return this.name;
    }
}

// 함수 를 그냥 호출했을때 와 new 키워드와 같이 호출했을때의 차이점 을 할수 있다. 

// 1. 함수를 그냥 호출했을때
Name('john'); // this is window, undefined 리턴

// 2. new 키워드와 함께 함수를 호출했을 때
new Name('john'); // this is Name{}, Name{name:'monkey', getName()} 리턴



var x = new Name('john');

x.getName(); // 'john'

  • 2.객체 생성자 함수의 활용 - 모듈화 와 프로토타입

    *기능별로 모듈화 시킨 독립적인 클래스 단위로 그루핑할때 생성자 함수를 활용할 수 있다.

    • 예를 들어 구글지도 UI를 만들 때, 화면에 보이는 기능 단위 즉 의미적으로 다른 기능이라면 (ex. 사진, 공유, 검색, 지도화면, 설정) 각각의 기능을 별도 모듈(클래스 단위)로 만들 수 있다.

// 모듈화 수도코드 예시
// 지도를 표현하는 영역 클래스

function Map(name){
    this.name = "john"
    }
    
// 지도를 검색하는 영역 클래스
function SearchMenu(){}

// 사진을 슬라이드 하는 영역 클래스
function ViewCurrentPhotos(){}


var oMap = new Map("john");

 // 여기서 setDraw 를 설정해준다.
Map.prototype.setDraw = function (){
    console.log(name + "그림을 그리네 ?");
}

oMap.setDraw() // john 그림을 그리네?
  • 3.객체 생성자 함수의 활용 - 모듈화 와 프로토타입



function Car(band,name,color) {
    // 인스턴스가 만들어 질때  실행될 코드들... 
}

// new 키워드를 통해 클라스의 인스턴스를 만들어낼 수 있습니다. 



// 1. 속성  : band,name,color , currentFuel,maxSpeed
// 2. 메소드  : refuel() ,setSpeed(), drive()



// ex


// 1. 클라스 함수 와 인스턴스 생성 

function Car(brand,name,color) { // Car() 는 클라스
	
	this.what_brand = brand; // 여기서 this 는 인자값이 드러갈 변수이름 (avante)
	this.what_name = name;	
	this.what_color = color;
}

// 2. 클라스 함수를 변수에 담고 파라미터 들어갈 값들 넣는다. 

let avante = new Car("GM","avante","black"); // 변수를 만든다 (인스턴스값으로 들어갈 )

// 3. 추가로 인스턴스를 생성 

Car.prototype.what_drive = function () { // Car() 인스턴스 생성 그리고 function 는 인스턴스 값  
    console.log(this.name + "가 운전을 합니다. ");
}


avante.what_name // 인스턴스 값 출력
// "avante"
avante.what_brand
// "GM"
avante.what_color
// "black"

avante.what_drive()  // 새로 생성한 what_drive 출력 
// jj 가 운전을 합니다. 

`tip`

let arr = [1,2,3,4,5]     // 배열 만들기 
let arr = new Array(1,2,3,4,5) // 배열 만들기  // Array클라스 안에 (인자값들) 




// ES6  에서는 클라스라는 키워드를 이용해서 정의 할수 있다. 


class car {
	constructor(brand,name,color) {
	
	// 인스턴스가 만들어질 때 실행되는 코드
		}
}

Instantiation Patterns

  • 자바스크립트에 Class가 나오기 전에 사용하던 4가지 class 선언 방식 이것이 바로 Instantiation Patterns 방식이다.

  • 함수를 이용한 객체 생성 방식을 이용한다.

  • Object 를 생성하는 4가지 방법

    1. Functional
    1. Functional Shared
    1. Prototypal
    1. Pseudoclassical

1. Functional


let Car = function() {
  let printingInstance = {};
  printingInstance.position = 0;
  printingInstance.move = function() {
    this.position ++;
  }
  return printingInstance;
}

let car1 = Car();

car1 {position: 0, move: ƒ} 
car1.move() // position 1 증가하한다 
car1 {position: 1, move: ƒ} 
car1.move() // position 1 증가하한다 
car1 {position: 2, move: ƒ} 
car1.move() // position 1 증가하한다 
car1 {position: 3, move: ƒ} 
car1.move() // position 1 증가하한다 
car1 {position: 4, move: ƒ} 


// position 초기값을 정해줄 수도 있다


let CarType2 = function(position) {
  let printingInstance = {};
  printingInstance.position = position;
  printingInstance.move = function() {
    console.log(this); 
    this.position ++;
  }
 return printingInstance;
}
 
var car2 = CarType2(2);
car2.move();
car2 // { position: 2, move: ƒ }
car2.move(); 
car2 // // { position: 3, move: ƒ }

2. Functional Shared

  • Functional Shared라는 방식을 사용한다면, someMethods라는 객체에 있는 메소드들의 메모리 주소만을 참조하기 때문에 메모리 효율이 좋아진다

// 3. // someInstance와 someMethods를 합치는 extend 함수를 만들어 Car 함수 내부에 넣는다. 

let extend = function(to, from) { 
  for(let key in from) {
    to[key] = from[key];
  }
}


// 2.메소드를 담아줄 객체를 생성.

let someMethods = {}; 
someMethods.move = function() {  // 모든 메소드는 someMethods에 담긴다. 
  this.position ++;
}


//  1. 먼저 Car 함수를 선언해 줍니다. 

let Car = function(position) { 
  let printingInstance = {
    position : position,
  }
   
  extend(printingInstance, someMethods); // Car함수 내부에서 합쳐준다 
  return printingInstance;
}


var car1 = Car(5); // 공장처럼 찍어낸다.
var car2 = Car(10); // 공장처럼 찍어낸다.
  1. Prototypal

왜 이방식을 쓰냐? 귀찬게? 이전의 Functional 방식은 인스턴스를 생성할 때마다 모든 메소드를 someInstance에게 할당하므로, 각각의 인스턴스들이 메소드의 수 만큼의 메모리를 더 차지하기 때문입니다.

However, Functional Shared라는 방식을 사용한다면, someMethods라는 객체에 있는 메소드들의 메모리 주소만을 참조하기 때문에 메모리 효율이 좋아진다


// 1. 먼저 Functional Shared 비슷하게 메소드를 담아둘 객체 생성 

var someMethods = {};
someMethods.move = function() {
 this.position += 1;
};


// 2. Car 라는 함수 선언해 준다. 

var Car = function(position) {
	var printingInstance = Object.create(someMethods);  //기존에 만든 someMethods를 상속해버린다. 어디에? 여기에
    printingInstance.position = position;
    return printingInstance;
};

var car1 = Car(10);
car1 // {position: 10} // 이렇게 나온다.

// 메소드 move 는 어디갔냐? 
console.dir(car1) // 하면 
// position: 10
//__proto__:
//	move: f()

car1.move() 
car1 //  {position: 11}
car1.move() 
car1 //  {position: 12}
car1.move() 
car1 //  {position: 13}
    1. Pseudoclassical
// 1.먼저 Car 함수 생성
var Car = function(position) {
    this.position = position
    }

// 2. 그다음 prototype 에 메소드를 추가한다. 

Car.prototype.move = function (){
    this.position ++;
 }



var car1 = new Car(10) // 꼭 new operater 를 붙여야 한다. 
car1 // {position: 10} // 이렇게 나온다.

// 메소드 move 는 어디갔냐? 
console.dir(car1) // 하면 
// position: 10
//__proto__:
//	move: f()

car1.move() 
car1 //  {position: 11}
car1.move() 
car1 //  {position: 12}
car1.move() 
car1 //  {position: 13}

자료구조란 ?

  • 데이터에 편리하게 접근하고, 변경하기 위해서 데이터를 저장하거나 조직하는 방법 을 말한다. 모든 목적에 맞는 자료구조는 찾기 어렵다.

Stack

Stack 이란 ?

  • 마지막에 쌓인것이 먼저 먼저 나오는 자료구조
  • Last In First Out => L I F O 이렇게 표현된다.

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 4.43.04 PM.png)

Property

* top : 가장 최근에 들어간, 맨 위의 값
* maxSize : 스택의 최대 할당 크기
* storage : 스택이 가지고 있는 데이터들의 모음

method

* 1. push : 맨 뒤에(위에) 삽입
* 2. pop : 맨위 제거
* 3. size : 크기 확인

오류

  • stack이 꽉차있는데 데이터를 삽입하려고 하면 Stack Overflow가 발생해 데이터가 들어가는 것을 차단한다.

  • 재귀함수가 멈추지 않을떄 자바스크립상에서 이를 방지하기 위해 Maximum call stack size exceeded 발생 시킨다 이것은 Stack Overflow에 기반한 오류로 볼 수 있다.

  • Stack이 없는데 값을 꺼내려고 하면 Stack underflow가 발생한다.

Queue

Queue 이란 ?

  • 먼저 들어간 데이터가 먼저 나오는 자료 구조.
  • First In First Out => F I F O

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 4.47.58 PM.png)

property

* front : 가장 먼저 들어간, 맨 밑의 값
* rear : 새로운 데이터가 들어갈 인덱스 (가장 최근의 인덱스 + 1)
* storage : 큐가 가지고 있는 데이터들의 모음

method

* 1. enqueue : 맨 뒤에(위에)삽입
* 2. dequeue : 제일 앞에 빼기

오류 발생

  • 만약 큐데이터가 비워있는데 삭제한다고 하면 오류가 발생한다. Queue Underflow 라고 한다.
  • 만약 큐데이터가 꽉 차있을 경우 삽일 하려고 한다면 오류가 난다. Queue Overflow 라고 한다.

Linked List

Linked List 란?

  • 연결리스트는 각 데이터들을 포인터로 연결하여 관리하는 자료구조
  • 데이터값이 앞과 뒤로 연결되있다.
  • 노드들의 모임
  • 배열은 추가삭제가 느리지만 인덱스 조회가 빠르고 Linked List 는 추가삭제는 빠르지만 인덱스의 조회가 느리다.

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 5.03.37 PM.png)

연결 리스트를 사용할 때의 장점

  • 데이터를 차례대로 순회하면서 연산하기 좋음

  • 순회 도중에 새로운 데이터의 삽입, 삭제에 용이함

  • 배열과는 달리 데이터의 개수를 모르는 경우에도 별도의 비용없이 추가할 수 있음

연결 리스트를 원형으로 연결할 때의 장점

  • 반복적인 순회에서 연결리스트의 끝을 체크해야할 필요가 없음

  • head같은 메타데이터가 필요하지 않음

  • 이로인해 시간, 메모리, 코드 모두 이득을 볼 수 있음

Property

HEAD : 첫 번째 노드를 지정하는 값
TAIL : 마지막 노드를 지정하는 값

Method

addToTail 추가 : 마지막 번째 노드에 데이터를 삽입
removeHead 삭제  : 첫 번째 노드를 삭제
contains 탐색 : 연결 리스트가 주어진 값을 포함하고 있는지 확인

Graphs

Graphs 란?

  • 노드(node)와 노드를 연결하는 간선(edge)로 이루어진 비선형 자료 구조
  • 버텍스(vertex)와 노드를 연결하는 아크로 이루어진 비선형 자료 구조
  • 그래프에서는 노드를 버텍스, 엣지를 아크라고 부릅니다.
  • 예를 들어 지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방통행길), 선수 과목 등이 있다.
  • 오일러 문제(다리 건너기), 길찾기 알고리즘, 최단거리 알고리즘(다익스트라,벨만포드)

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 5.35.39 PM.png)

Graphs 종류

* 무방향 그래프
* 정방향 그래프

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 1.34.31 PM.png)

Property

node : 그래프를 구성하는 노드들
edge : 노드들을 연결하고 관계짓는 간선들
nodes : 노드들을 담고 있는 데이터 배열

Method

addNode : 그래프에 노드를 추가한다.
removeNode : 그래프에서 노드를 제거한다.
addEdge : 노드와 노드 사이에 간선을 추가한다.
removeEdge : 노드와 노드 사이의 간선(관계)를 제거한다.
hasEdge : 노드와 노드 사이에 간선(관계)가 있는지 확인한다.
contains : 그래프가 주어진 값의 노드를 포함하고 있는지 확인한다.
forEachNode : 주어진 함수를 그래프가 가지고 있는 노드 각각에 대해 실행한다.

그래프를 코드로 표현하는 2가지 방법

    1. 인접 행렬 그래프
    1. 인접 리스트 그래프의 두가지로 나눌 수 있다.

인접 행렬 그래프

장점: 직관적이며 쉽게 구현 가능
단점: 불필요한 정보의 저장이 많으며, 그래프의 크기가 커지면 메모리 초과가 발생할 수 있음
구현: int형의 2차원 배열을 주로 이용하며, 이동할 수 있으면 1, 없으면 0으로 표기함

인접 리스트 그래프 - “갈 수 있는 곳만 저장”

장점: 필요한 정보만 저장하여 메모리 절약 가능
단점: 인접행렬에 비해 다소 어려움
구현: 리스트(List)나 벡터(Vector)등의 자료구조를 이용하여 각 정점에서 이동가능한 정점들을 저장(List나 Vector를 이용한 2차원 배열이라 생각하면 이해하기 쉬움)

길찾기 알고리즘

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2020-01-04 at 2.17.29 PM.png)

Tree

Tree 란?

  • 트리는 노드(node)들과 노드들을 연결하는 링크(link)들로 구성됨
  • 부모-자식 관계를 이루는 노드들로 구성된 자료 구조
  • 컴퓨터 directory 구조 비슷 특정한 파일을 찾을때 폴더안에 폴더가 있고 그안에 파일이 있다 이러한 구조를 Tree 구조라고 한다.(조직도)

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 5.10.35 PM.png)

Tree 종류에는 4가지가 대표적으로 있다.

  • 1.이진 트리 (binary Tree) 란?
  • 2.편향 이진트리(skewed binary tree)란?
  • 3.포화 이진트리(full binary tree)란?
  • 4.완전 이진트리(complete binary tree)란?

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2020-01-04 at 2.52.31 PM.png)

  • 1.이진 트리 (binary Tree) 란?

    • 이진 트리에서 각 노드는 최대 2개의 자식을 가진다.

    • 이진트리인 경우 왼쪽서브트리와 오른쪽 서브트리로 구성된다. 여기서 중요한점은 왼쪽과 오른쪽 서브트리를 확실하게 구분한다는 것이다.

  • 2 편향 이진트리(skewed binary tree)란?

    • 한쪽으로만 되어있는 한쪽 자식만 가지고 있는 것
    • liked list 와 같이 생각할수 있다.
    1. 포화 이진 트리(Full Binary Tree) ?
    • 모든 레벨이 꽉 찬 이진 트리
    1. 완전 이진 트리(Complete Binart Tree) 란?
    • 포화 이진 트리처럼 모든 레벨이 꽉 찬 상태는 아니지만, 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리

용어

  루트 노드(root node) : 부모가 없는 노드. 트리는 하나의 루트 노드만을 가진다.
  단말 노드(leaf node) : 자식이 없는 노드이다.
  내부(internal) 노드 : 리프 노드가 아닌 노드.
  링크(link) : 노드를 연결하는 선 (edge, branch 라고도 부름).
  형제(sibling) : 같은 부모를 가지는 노드.

Property

nodes : 값과 자식들로 이루어진, 노드들의 모임
edge : 노드들을 서로 연결하는 간선

Method

addChild() : 주어가 되는 노드에 자식 노드를 추가한다.
removeNode() : 주어진 값을 가진 노드를 삭제한다.
contains() : 주어진 값을 트리에 있는 노드들이 가지고 있는지 확인한다.

binary search tree

  • 이진 탐색 트리(binary search tree)는 이진 트리 기반의 탐색을 위한 자료 구조이다

이진 탐색 트리는 4개의 조건이 있다

  • 바이너리 서치 트리는 세 가지 특징을 가지고 있습니다.

      1. 트리의 각 노드가 갖는 자식 노드의 수가 2개 이하가 되어야 합니다.
      1. 부모 노드의 왼쪽 하위 트리에 있는 모든 노드의 데이터는 부모의 데이터보다 작거나 같아야 합니다.
      1. 부모 노드의 오른쪽 하위 트리에 있는 모든 노드의 데이터는 부모의 데이터보다 커야 합니다.

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 5.16.03 PM.png)

  • 바이너리 서치 트리를 순회하는 방법에는 두 가지가 있습니다.
  • DFS (깊이 우선 탐색, Depth-First Search):

루트를 시작으로 점차 깊이 들어갔다가, 가장 깊은 depth에 도달했을 때 다시 나오고, 또 다시 깊이 들어가는 방식을 반복하며 전체 트리를 순회합니다.

  • BFS (너비 우선 탐색, Breadth-First Search):

sibling을 먼저 탐색하고, 그 후 다음 depth로 들어가 해당 depth의 slibling을 탐색하는 식으로 전체 트리를 순회합니다.

알고리즘 방법 (추가학습)

<탐색 알고리즘>
<삽입 알고리즘>
<삭제 알고리즘>
이진 탐색 트리의 시간복잡도 분석
이진 탐색 트리에서는 최상의 경우 시간복잡도가 O(logn)인 탐색을 할 수 있다.

Property

left :  루트노드의 왼쪽에 있는 노드들  오른쪽보다 작은 
right : 루트 노드 의 오른쪽에 있는 노드들 왼쪽보다 큰 
value : 노드의 값

Method

insert : 주어진 값으로 노드를 만들어, 맞는 위치에 삽입
contains : 트리를 반복하여 주어진 값이 있는지 확인
delete : 노드를 삭제하고 트리 위치를 조정

삭제하는 3가지 방법

  • 1.맨밑에 지울때 리프한번의 연산 O(1)

  • 2.자식이 한개인노드를 지울때 두번의 연산 일어난다. O(n)

  • 3.자식이 2개이상인 노드를 지울때 이자리에 올려줄 친구를 찾는다.??? O(n)

Hash Table

Hash Table 란?

  • 데이터의 효율적 관리를 목적으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수입니다. 이 때 매핑 전 원래 데이터의 값을 키(key), 매핑 후 데이터의 값을 해시값(hash value), 매핑하는 과정 자체를 해싱(hashing)라고 합니다.

  • 값을 가공하기 위해서는 해쉬 함수가 필요하다

  • 해쉬 함수란?

    • 키값을 (Dog) 을 넣으면 고유의 값(!@#1)이 나와서 hi 를 찾게 해준다.
    • 0 부터 key를 담은 값의 length 만큼만 반환시켜줄수 있어야 한다.
    • 언제든지 key 를 넣었을때 같은 값이 나와야 한다.
    • 어떠한 저장도 할수 없다. 기억을 가지고 있지않고 그때그때 값을 내밷어야 한다.
    • 근데 만약 fox 를 넣었는데 Dog 을 넣었을때 고유의 값 고유의 값(!@#1) 가 나온다면 충돌이 난다.
    • 그래서 고유의 값(!@#1)이 저장되에 있는곳에 0번째에 Dog > 1번째의 hi 를 가르키게 해주고 저장해놓고 0번째의 fox > 1번째의 hello 를 저장해놓게 된다면 고유의 값(!@#1) 값에서 0번째들안에 fox 를 찾아 value 값을 반환해주게 하면 된다 !

특징

  • key,value를가지고 있는 것
  • 어떤 특정 값을 받으면 그 값을 해시 함수에 통과시켜 나온 인덱스(index)에 저장하는 자료구조
  • O(1)의 시간복잡도로 해결할 수 있다
  • 고유에 인댁스로 바로 접근할수 있기 때문에 빠르게 검색할수 있다.
  • 해시 테이블은 사전을 구현하는 가장 효율적인 자료구조이다.

주의

  • 해쉬 테이블은 원래 O(1) 를 자랑하는데 O(n) 이 될수 있다.

  • 내가 insert 한 값이 same bucket 에 들어가게 된다면 O(n) 이 된다.

  • when a hash table is growing, it resizes itself and every element must be rehashed

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2019-12-31 at 5.53.57 PM.png)

  • 스토리지 ?

  • 튜퓰 ?

  • bucket ? ![](/tutorial/2019-12-21-spint2_files/Screen Shot 2020-01-05 at 12.36.09 PM.png)

Property

limit : 한 슬롯(버킷) 안에 들어갈 수 있는 데이터의 최대 갯수이다.
storage : 데이터들이 저장되는 테이블이다.

Method

insert : 주어진 index로 테이블에 데이터를 추가한다.
retrieve : 주어진 Index로 데이터 값을 찾아 리턴한다.
remove : 주어진 키값에 해당하는 index에 들어 있는 값을 제거한다.

Complexity Analysis

Complexity Analysis : 복잡도 분석이다.

  • 복잡도 분석이란 무엇이냐?

    • 알고리즘이 문제를 해결하는데 얼마나 시간과 공간을 차지 하는지 나타내는 지표이다.

시간복잡도에서는 Big-O표기 할수 있다.

  • O(1) – 상수 시간 :

입력값 n 이 주어졌을 때, 알고리즘이 문제를 해결하는데 오직 한 단계만 거친다.

예 ) array lookup, hash table insertion

  • O(log n) – 로그 시간 :

입력값 n 이 주어졌을 때, 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다.

예 ) binary search(tree)

  • O(n) – 직선적 시간 :

문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가진다.

예 ) linked list, array search

  • O(n^2) – 2차 시간 :

문제를 해결하기 위한 단계의 수는 입력값 n의 제곱이다.

예 ) constant time operation inside two nested for-loops

  • O(C^n) – 지수 시간 :

문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱이다.

예 ) recursion 피보나치 수열 등등

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2020-01-02 at 11.35.18 AM.png)

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2020-01-02 at 11.35.32 AM.png)

시간복잡도의 예시

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2020-01-02 at 11.33.25 AM.png)

Arrays

  • lookup O(1)

인덱스를 알고있기때문에 바로찾을수 있다.

  • Assign O(1)

인덱스를 알고있기 때문에 바로 바꿔버릴수 있다.

  • insert O(n)

값을 추가하고 나머지 값들의 인덱스가 바꿔지기 때문에 시간복잡도가 늘어난다.

  • Remove O(n)

특정값을 제거하면 나머지 값을을 땡겨서 인덱스를 맞춰야 하기 때문에 시간복잡도가 늘어난다.

  • find(value) O(n)

값이 어디에있는지 찾으려면 모든 인덱스값에 접근해야 하기때문에 시간복잡도가 늘어난다.

Linked Lists

  • Lookup(Position) O(n)

특정 위치 를 찾으려고 한다.

인덱스를 알수가 없다 무조건 head 부터 시작해야 한다. head 부터 시작해서 차례대로 찾는다.

  • Find (value )O(n)

특정 값을 를 찾으려고 한다.

인덱스를 알수가 없다 무조건 head 부터 시작해야 한다. head 부터 시작해서 차례대로 찾는다.

  • Assign O(n)

값을 바꿔주려고 할때 그값을 찾으러 갈때 head부터 차례대로 가기 때문에 시간복잡도가 O(n) 이 된다.

  • insert O(1)

만약 내가 어디에 추가하고싶은지 알고있다면 O(n) 된다.

왜냐하면 기존 에 값의 next pointer 를 알고있기때문에 next pointer 를 내가 추가하고자 하는 값에 연결시켜주고 내가 많든 값의 next pointer 를 다음 값에 연결시켜주면 되는 것이다.

  • Removal O(n) or O(n)

head 처음에 값을 제거하려면 O(1)된다.

midle 중간에 값을 제거하려면 O(n) 된다.

왜냐하면 값을 제거하기위 next-poniter 를 옮겨주면 되지만 뒤에 poniter 를 가지고 있지 않기 때문이다. 그래서 찾아야한다.

하지만 Doubly_linked lists 에서는 insert 와 remove 는 O(1) 이된다 왜냐하면 이전에 pointer 와 다음에 poniter 둘다를 가지고 있기 때문이다.

Array % Singly-Linked List & Doubly-Linked Lists

array

  O(1) : lookUp
  O(n) : insert/remove

Singly-Linked List

  O(1) : insert
  O(n) : lookup, remove

Doubly-Linked Lists

  O(1) : insert/remove

여기서 주의해야하는 것이

Doulbly-linked Lists 는 각각의 노드들이 이전 다음 pointers 를 가지고 있기 때문에 공간 복잡도에서 조금 늘어나는 차이가 있다.

Trees

  • Find O(n)

각각의 노드를 검색해야하기 때문에 시간복잡도가 늘어난다.

루트부터 쫙 찾야아 한다.

Binary Search Tree

특정조건이 가지고 있다.

  • find O(log n)

특정값을 찾겠다고 하면

3번만에 확인이 가능하다.

빠른것이다.

만약 linked-list 처럼 형태가 만들어진다면 (일자형 ) find O(n) 되버린다.

이런경우를 방지하기 위해 Tree 구조를 틀어버린다.

![](/tutorial/2019-12-21-spint2_files/Screen Shot 2020-01-02 at 8.09.06 PM.png)

그림에 나와있는 것처럼 추가할때마다 벨런스를 에 맞겠 조정을 해주면 다시

find O(log n) 의 구조를 유지할수 있다.

  • 정렬된 구조에서 배열을 쓰지않고 binary search 구조를 쓰는 이유가 있을까요?

Array 는 메모리를 계속 차지한다.

Trees 구조는 linked-list 도 쓸수 있기때문에 구석구속 메모리를 쓸수 있어 효율적이다.

메모리 효율적인면에서 BST 가 더낳다.

Last updated on Apr 29, 2019